Tag Archives: fractions

#classroombookaday UPDATE: Week of January 7, 2019

Welcome back to school!  We are getting back into our routine after a fantastic holiday break and I’m excited to share another great week of reading in first grade!  Check out our wall and how fast it is filling up!

img_6553

As of January 11, we were at 266 books!

Check out the books we’ve added since last week! 🙂

You may or may not be able to tell that we are working on fractions, problem solving, persuasive writing, and also did some learning about penguins.  Going Places and I Built a House were included in some design challenges (which I will share soon!) and some were just for fun. :).

I have gotten a couple of suggestions for new reads, please continue to share your ideas for what we should read next! 🙂

**Sidenote: As I was adding the Twitter mentions for this post, I realized how many authors we read this week had written other books we already love!  Thank you, Laurie Keller, for writing Potato Pants!  Just realized you also wrote Arnie the Doughnut, which we loved form last year.  Genius!  And of course, I noticed when we read Mae’s First Day of School that it was the same author as Hannah and Sugar (you’re awesome, Kate Berube!), another one we love–which has a song we love from Emily Arrow! It’s worth a share here, since it’s so good. 🙂

 

Second Grade Math Warm-Ups: Week of May 2-6, 2016

I am a little bit late–sorry!  I forgot a few important pictures that I needed in order to properly share.  Hopefully you’ll still read (and learn with us!).  🙂

Monday

There’s not a lot to explain behind this one except that I wanted to continue to focus on the idea of a fraction being EQUAL pieces, not just the number of pieces in the denominator.  As you can see in many of the post-its, most kiddos understand this when they partition the cookie cake for 4 people.

IMG_1628-min

Tuesday

As I mentioned with a problem or two last week, kiddos are to have a basic foundation of groups and arrays to help them with further multiplication concepts in 3rd grade.  We played a game called Circles and Stars last week, which is basically where they roll a dice twice, once drawing circles and then filling each with the 2nd number’s worth of stars.  Then they figure out an equation to go with the model as well as how many stars there are altogether.  I wanted to build on this idea and see what they’d do with a new problem.  As is seen on their answers, they almost all drew circles with stars (or dots).  I wanted to help them see the same idea as an array, as well, so I connected the equation to brownies (so they pan/array would make more sense).

FullSizeRender 156-min

Wednesday

Somewhere I had saved a picture of my original problem which looked like this (the purple writing on the chart): If I had a pan of brownies that had 7 brownies on one side and 5 brownies on the other, how many would I have?  When I looked at the answers, I was completely baffled as to why so many had answered 6X2=12.  We had a great decision about how they used 7+5=12 and then made a multiplication equation that matched.  There were also some pretty interesting models/pictures of the equation, too, so I drew an array to show what I meant.  Once they saw it, they could see what I meant, but we agreed that the problem I had written didn’t lead them to that understanding.  I asked them to help me figure out how I could have better written the problem so that they could have seen what I meant.  We worked to revise the question so it made more sense.  This was a GREAT conversation both about math and revision, which is something Rm. 202 friends know happens ALL THE TIME, not just in writing.  They did a super job of helping me redesign the warm-up so that it better matched what I wanted to know.

FullSizeRender 159-min

Now it reads: If I had a rectangular pan of brownies that had 7 columns of brownies on the long side of the pan, and 5 rows of brownies on the other, how many would I have in the whole pan?  Draw a picture.   Great work on the writing and the math, Rm. 202 friends!

Thursday

IMG_1786-min

Friday

We’re still working on many concepts all at once, and solidifying our understanding of them.  Love my little speech bubble?  We always talk about how the numbers in the problem scream at us to tell us which strategy is most efficient for them, so it just seemed fitting. 😀

 

Second Grade Math Warm-Ups: Week of April 25-29, 2016

We have been on a roll with warm-ups lately, and maybe since we’re still talking about many different things, they’ve given us a way to keep all the balls in the air.  Love that.  Enjoy! 🙂

Monday

One of the topics we’re working on right now is the foundation of fractions, and understanding about equal parts.  This warm-up led to a GREAT conversation about how 1/5 is always a 1/5, but the actual portion that is being considered changes based on the whole.  Oh, and we were all hungry when we were finished. 🙂

IMG_1619-min

Tuesday

It seems like addition and subtraction is a never-ending concept with 2nd graders, and we’re still working on it.  Oh well, as long as it takes.  School year’s not over yet and they can get it! Here was another opportunity to practice.

Wednesday

Ok, so I need to explain that that picture is a pizza, not a target.  It’s based on a picture we had looked at the day before in a math conversation.  It was based on an 8-slice pizza and how we could share it fairly if twice as many people showed up for our party.  This was the way one group suggested we do it, and we had to discuss whether we agreed if it was fair.  Which piece would you want? 🙂

IMG_1573-min

Thursday

We had a FABULOUS walking field trip on Thursday at the time we normally do math warm-ups, so didn’t have one that day.  We had a great day in the park and a movie instead! 🙂 (Don’t worry–it was connected to our curriculum!)

Friday

Another topic (which I found a way to weave into this conversation, too!) is the foundation of multiplication.  We told many stories of groups of things with this one.  Great thinking, Rm. 202 kiddos!

IMG_1626-min

 

 

Second Grade Math Warm-Ups: Week of April 18-21, 2016

This was a 4-day week at school, but since we’ve moved our MWU to the afternoon (instead of first thing in the morning), it has seemed it’s been easier to make them happen every day.  Maybe it’s just because of the unit we’re in, too, but our conversations about them have been SUPER POWERFUL lately.  Can’t imagine teaching without this part of our day!

Monday

I definitely should have taken a before and after picture of this one.  The circles were all filled up with post-its when we sat down to talk, but we had to work through them and decide which ones sounded like things mathematicians would say about these polygons.  Many of them were vague or didn’t use mathematical terms.  They said things like “they’re different” or “they’re the same.”  We talked through the definition of polygon (hence the words over there) as well as what some mathematical terms were that we should listen for as we narrowed down the choices.  This idea of comparing is something that students are expected to know how to do independently with two different polygons by the end of the unit, so trying some together along the way was crucial.

IMG_1512-min

Tuesday

This one matches up with both some work on shapes we had done earlier (names and attributes), as well as a replay of the question from the day before to see how they’d do in the same situation with different shapes.  The number of specific, mathematical responses was much greater this time and we had less work to do to make our Venn Diagram make sense.

IMG_1511-min

Wednesday

This question has a great story to tell (which is SO long and involved I’ll be nice and put it in a different post!), and really gave us lots of math to chew on.  And I thought I would be an easy one.  Those are always the problems that surprise me.

IMG_1515-min

Do you see the marks on the word HALF up there? Here’s a close-up:

IMG_1516-min

We’re applying our knowledge of lines, angles and polygons everywhere we look!  This wasn’t even part of the question, but of course was a great part of the discussion!

Thursday

After all our hard work (which I hope you’ll pop over and read about), I wanted to see if they could remember and apply it to a similar but new situation.  Most could see how the knowledge we had gained the day before about halves applied to thirds (and therefore to fourths, fifths, sixths, etc.).

IMG_1517-min

What did you work on as a mathematician this week?  What warm-ups would you suggest to us that include angles, polygons or fractions?  We’d love to try some more! 🙂

Math Warm-Ups: First Grade Version–Week of 12-1 to 12-5

For years in 5th grade I posted about Math Warm-Ups and how we used them to get our brains ready for flexible math thinking every morning.  Last year I didn’t use them much–for one reason or another–and this year they didn’t make sense until just recently.  So here we go–join us to see how Math Warm-Ups work with young mathematicians and how we use them to stretch our brains!

Week of December 12-1 to 12-5

Monday

Wait–Monday we didn’t have a Math Warm-Up.  Partly because it was the first day after a really long weekend and also because we had some unexpected freezing rain during the morning rush and it took me 2 1/2 hours to get to school that day!  I did anything but rush to school.  Here’s a picture of how fast we were going at one point.  And believe me, I was being really safe while I took this pic:

 

See that? I think it says 2 miles an hour. On the highway. Seriously.

See that? I think it says 2 miles an hour. On the highway. Seriously.

Tuesday

This was the first day of Math Warm-Ups so I asked a question that I knew everyone could answer easily, as the point was to teach the purpose and procedure more than focus on a math concept.  Still, we were able to pull in many things we’d been working on in math during our conversation about this warm-up.

CAM01121

Now that I look at that picture, I wish I would have taken one right after we put all the post-its on it, because it was much messier, and that’s actually part of the conversation we had about what we could do with the data we had collected: someone suggested that it needed to be more organized.  I also asked them what question we could answer with the information we had up on the easel.  There were several good ideas, one of which was “Do we have more 6YOs or 7YOs in our class?,” hence why we ended up with two columns of notes.

           CAM01086    CAM01085

It was great to watch and listen when we started to analyze the notes and figure out how many of each age there were: they used what we’ve been learning about grouping objects to count, and recognized that I put them into the same shape as the 10 frames we’ve been looking at lately.  They were similar to what our math racks look like, too, and they quickly and easily saw that there were 7 6YOs on this day and 10 7YOs.  We talked about other questions we could answer, and also talked briefly about how this data could change based on the day (we had 3 friends absent).

Wednesday

CAM01120

Another one I knew most could answer easily, but a little harder than yesterday.  The focus today was on making sure we followed all the directions of the warm-up: answering the WHOLE question and putting our name on our post-it.  There were still some who did not, so we made sure to talk about that when we reviewed this question during math.  The words LESS and GREATER were also a focus, as was writing the number the way it should actually look–with digits in the right places AND going the right direction (which is still tricky for some friends at this point in 1st grade!).

Thursday

CAM01119

We’ve been working on flexibility with combinations up to 20, as well as most recently practicing doubles and doubles +1.  This was interesting, then when most kids put 10+9 as their answer (which is probably the easiest combination to figure out).  I noticed many who wrote combos that DIDN’T equal 19, so the conversation was around accuracy as well as how they figured out their answer.  It also told me that as a whole, we need some more practice on this skill!

Friday

CAM01118

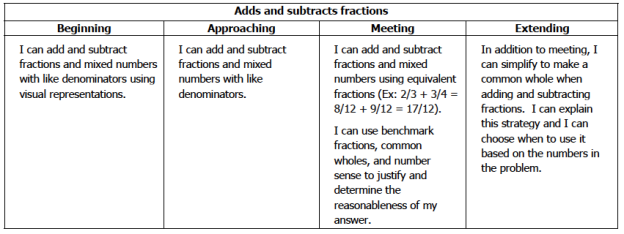
This question was just one to see where we were with fractions, as we’re about to finish up that unit.  The benchmark is just that kids understand 1/2s and 1/4s, but the “extending” on our rubric is 1/3s and I was pretty sure most kids could tackle that as well.  And boy was I right!  Now…I am not entirely sure if kiddos answered these on their own (like they’re supposed to) or if they worked together, so there’s more work to be done, but for the most part you can see that most of those rectangles (which is also part of this unit) are divided into 3 equal pieces!  Even the way I worded the question gave me some information–info that I didn’t expect–when someone said, “I can’t just draw 1 line and make thirds.  Can I draw more than 1?”  Obviously that friend knew what was going on!  I hadn’t done that on purpose, and so made the change on the chart for the rest of the friends who completed it.

This is our first try with warm-ups this year and I am excited to see where they go!  Great job, Rm. 202 friends!  You did an AWESOME job!

Teachers–What kinds of math warm-ups have you done with your class?  Have you tried them with 1st graders?  How did it go? We’d love to hear about what’s going on in your class!  Parents–did you hear about Math Warm-Ups from your kiddo?  What were they saying? 🙂

Fractions with Fosnot and Flex Time

Remember last year when I told you all about Feast Week?  Well, it’s that time of year again, for fractions at least, but not–it seems–for Feast Week.  Instead, we’ve begun using some AMAZING new resources from Cathy Fosnot, that have helped our mathematicians think of fraction parts in a whole new way.

My favorite part of math right now is the addition of Fraction Flex Time (man, it seems like we need to add a cute name to every thing fraction related…).  After we finished the investigations in our Fosnot unit (which included figuring out the Best Buys, Oatmeal Problems and Gas Tank problems), our team sat down to figure out how to divvy up our kiddos between the 7 teachers we have (Yes, I said SEVEN!! Isn’t that FABULOUS!! ??), based on the information we’d gathered during our first few weeks of study.  We made the groups small and intentional, and we planned for intense teaching and practice.

Although the pacing and strategies are a little different based on the groups’ need, the goal is the same (based on our district rubric):

Screen Shot 2013-11-19 at 9.03.25 PMJust like I shared in my post about our visit from Kara Imm from Mathematics in the City, number strings have become our new best friend.  I mean, honestly, before this year I really didn’t spend much time on them, but now I am not sure I can go a day in math without one–they just have such HUGE bang for their buck.  Just the other day we spent 45 minutes doing a number string together.  It sounds like a long time, maybe, but in that 45 minutes (during which my small group of friends was TOTALLY ENGAGED!), we were able to touch on the clock model, common denominators, reducing fractions, equivalent fractions, improper fractions and mixed numbers.  So cool!

I have heard such positive feedback from my class since we’ve been doing flex time. Most mention that they love the small numbers, the focused nature of the lessons and the time they get to spend with the teacher.  I agree, friends, I’m loving all those things, too!

My favorite thing from our lessons lately  is all of the “lightbulb moments” that I can actually see happen.  It’s so great to see that look of AHA! on a kiddo’s face, and how often these moments even have a sound.  All of the “ahs” I’ve heard lately have definitely made my days.

What do you think about fractions?  How do you think you would react to Fraction Flex Time?  Do you think you’d like it?  Please leave your feedback. 🙂

 

I Speak Greek When I Teach Math–PART 2

Wow–I’ve been doing a horrible job with updates lately!  I’ve left this one hanging for over a week, and I’m sure you were waiting on the edge of your seat to hear the rest of the story, right?  Well, thanks for being patient. 🙂   The “rest of the story” will actually end up being told in two more parts.

Remember how we were working with a problem about ranch dip and I was baffled by what was going so wrong?

Screen Shot 2013-04-17 at 8.55.41 PM

Ranch dip problem, part 1

Part 2

Part 2

Well, what I don’t think I told you last time was that I had a conversation with a colleague of mine, who happens to be a fabulous math teacher, too, and we agreed there could have been many reasons why this was trickier than I had intended.  I decided to tackle these issues one at a time.  The first one we thought of was related to the context.

I think I may have taken for granted the fact that my kids would know about teaspoons, tablespoons and just the whole act of mixing it all together.  There were actually several kiddos who could not relate to what I was talking about with making the dip, so I decided to fix that problem.  I hoped that using the recipe would help them better understand what I was asking them to figure out.  So we got cooking!

IMG_0748

First, we reviewed the recipe and talked ingredients so we made sure we knew what to do. See how handy our iPads are for jobs like this? 🙂

IMG_0751

Sorry, this ones a little blurry, but we’re smelling the spices the recipe called for: onion powder, garlic powder, parsley and dill. Many hadn’t ever seen these before!

IMG_0754

Oh, and there’s basil in it, too! Smells yummy already!

IMG_0756

The recipe calls for sour cream, but I decided to use plain yogurt instead. Man, I must have been stirring fast!

IMG_0757

We discovered another part that was important (and in many cases missing) knowledge–knowing the difference between the sizes of teaspoons and tablespoons. Knowing that there are 3 teaspoons in a tablespoon was necessary for use in the final answer, but this was hard for some kids to image without seeing it.

IMG_0760

Spice mix ready to be stirred!

IMG_0764

We needed a 1/2 cup of yogurt for every tablespoon of spices.

IMG_0768

Looking good!

IMG_0774

I forgot a knife. 😦 Cutting a cucumber with the back of a fork is harder than it looks! Eventually I made it happen, though. 🙂

IMG_0776

Yum! Ranch dip with cucumbers and Triscuits for our morning Math snack!

So while my cooking class didn’t solve every problem we were having (which I’ll tell you about in Part 3), I do think it gave many of them the ability to make connections they were unable to make before.  And there is so much math (and science) in cooking and baking, I don’t know why we don’t do more of it.  TOTALLY wish my classroom had a kitchen!  It has also made me and my team think about how we want to purposefully involve more of these types of activities into our classes for next year.  We’re thinking it would be a great addition and preparation for next year’s Feast Week, too.

How do you use cooking in your classroom?  What connections do you make for your kiddos to math and science?  Or maybe even reading and writing? We’d love to hear your thoughts and suggestions as we make plans for next year. 🙂

I Speak Greek When I Teach Math

Or maybe it’s Spanish or Chinese or Pig-Latin, but today I felt like I was definitely not speaking English to my kiddos during math.  Meaning no one understood what I was trying to explain, and many kids ended up more confused than when we first started.  WHAT?  It’s not like I’m new at this, nor to the topic.  We were even working on a problem that I made up!  Needless to say, we all wanted to throw in the towel, or rip up our papers and start over.  Or something else that you shouldn’t do when you’re frustrated.  And no, in case you’re wondering–we didn’t.  But we did put the problem away until tomorrow when we’re fresh and can tackle it again.  And I am already armed with a different plan for how to address it, but am hoping you can help me, too!  (And by the way, after how fabulous the first round of problems-with-posters went the other day, this was all the more mind boggling!)

Ok, so I’m hoping that you can help me figure out what might be making my friends so confused.  Here is the problem that we were working on yesterday and today:

Screen Shot 2013-04-17 at 8.55.41 PM

This problem is 1) based on a real-life problem, 2) uses math skills we already have (or at least that are not new!), and 3) really just focuses on making sure they use clear and concise notation to record their solution and thoughts.

Part 2

Part 2

PLEASE give me feedback on parts you see that may  have tripped them up.  After working on it for two days, I see a couple of things, but I really expected this to be a rather simple fraction problem; the difficulties they were having were not ones I had anticipated.  My hope was they could focus on the poster part, as a prep for how they’d answer questions as we start testing next week.  Instead, now they’re all convinced that math is hard and confusing.  Pretty much a teacher fail, huh? 😦

Thoughts?  Oh, and I guess it’s a given that I want you to be nice.  Truthful, but nice, please. 🙂  And maybe you could even tell me what you think the answer is.  That might help me see if the problem reads the way I intended it to.  THANK YOU, FRIENDS!

Math Warm-Ups April 8-12, 2013

Wow–how has it been a whole month since I last posted math warm-ups?  Oh, yeah, because MARCH was crazy–including a SNOW DAY and SPRING BREAK right next to each other.  And not that April is any less busy, but at least this week could be considered somewhat normal.  Oh, not it wasn’t–I had a sub on Tuesday.  But hey, what’s normal anyway, right?  Regardless, here are some recent math warm-ups I haven’t shared yet.

First of all, a couple from last week:

This one was to help discuss fraction place value, and also to help us talk about writing clear and concise answers to questions like these (in preparation for MAP testing in just over a week).

This one was to help discuss fraction place value, and also to help us talk about writing clear and concise answers to questions like these (in preparation for MAP testing in just over a week).

Can you tell I ran out of paper and didn't have a chance to get more for a couple of days? Sorry. :) This one is another place value one, hoping that students would see the relationship between money and fractions, and how they can just "move" the decimal (by multplying by 10), rather than having to use the algorithm to solve the problem.

Can you tell I ran out of paper and didn’t have a chance to get more for a couple of days? Sorry. 🙂 This one is another place value one, hoping that students would see the relationship between money and fractions, and how they can just “move” the decimal (by multiplying by 10), rather than having to use the algorithm to solve the problem.

This week’s warm-ups:

Wednesday

We needed to reminded (again) about equivalent fractions, as well as their tie to decimals.

We needed to reminded (again) about equivalent fractions, as well as their tie to decimals.

This one came right off of our Edison benchmark practice from this month. We're using the problems on that assessment to help us analyze the "why" of the ones we get wrong. This can help us not make those same mistakes again the next time we encounter them.

This one came right off of our Edison benchmark practice from this month. We’re using the problems on that assessment to help us analyze the “why” of the ones we get wrong. This can help us not make those same mistakes again the next time we encounter them.

This is another Edison problem, but I changed the numbers. Many students are still not remembering to make the denominators the same before they add. This one also elicited great conversations around simplifying answers--both how and why here as well.

This is another Edison problem, but I changed the numbers. Many students are still not remembering to make the denominators the same before they add. This one also elicited great conversations around simplifying answers–both how and why here as well.

 

I’m hoping I’m back in the routine of posting warm-ups.  Sorry if you’ve missed them! 🙂

 

 

Math Warm-Ups February 25-March 1, 2013

Last week was a little crazy, so we only had three warm-ups that stretched all throughout the week.

Monday

IMG267We came back to division (again) this week, as it’s a skill that many kiddos still have trouble with, even at this point in the year.  We have another unit of it in a couple more weeks, but we need the practice nonetheless.  The difference, too, this time is that we’re working on using a different strategy.  In the past–like when we were first learning how to divide–we thought about the number as a whole, and worked to find groups inside of it, rather than using the traditional algorithm.  Our focus was on understanding what division means, and we incorporated what we knew about multiplication as much as we could, as well.  This time, we’re trying to use the traditional method–still connecting to multiplication–but just organizing our thinking and our numbers in a different way.  We have been talking about reasonableness of answers, too, and use estimation to help us determine if our answers make sense.

 

The Rest of the Week

IMG269The rest of the mornings during the week were busy, we we actually took a couple of days to work through these problems.  You’ll notice a second division problem and then a good ‘ole adding fractions problem because we’re still fuzzy on this concept.  But truly, this is what is perfect about Math Warm-Ups–being able to easily revisit concepts that we need more time with.