Today’s ActivActivity is related to the Math Warm-up we had the other day:
Your job today is to come up with a story that uses FRACTIONS and has an answer of 3/4. Work together with your group to write one, and if you have time after that one, write another! Leave your story in the comments for this post, and be sure to leave your names!
The first parts of our Feast Week journey can be found here, here, and here. 🙂
Do you know Murphy? Isn’t it his law that says that anything that can go wrong will? Well he was present on the third day of Feast Week….
By Wednesday we were supposed to be ready to get our budget proposal to Mrs. Sisul so that we could be ready to shop on Thursday. That was the plan, but then the plans had to change.
Like I mentioned before, we had decided to make 5 yummy appetizers. We had figured out our shopping lists and figured out how much one batch of our goodies would cost. And then we started multiplying. And realized we were in trouble…
We first figured out how to change our recipes to feed 20 (before we figured it out for 85) and we noticed something:
We were using a favorite recipe of mine (from Catherine at weelicious.com) as an example and were figuring out how much of everything we’d need to feed 20, which meant we had to multiply our numbers by 5. It was pretty easy work since most of the ingredients were cans or whole numbers. When we got to the olive oil we got to display our fabulous fraction knowledge to create 5/3 which we simplified to 1 2/3 cups.
Ok, so all was well until we talked about how much it would cost us. We started sharing our numbers from the day before for single batches of each recipe. Some were around $5, but one was close to $15 for just one small amount. We quickly figured out that if we were going to create the amount we needed for 85 people, we’d be multiplying the original numbers by 40! That suddenly sounded really expensive…
We went back to our tribes and revisited our numbers. After adding together the total amounts for all five appetizers, to feed all of us we were going to be spending over $500! Obviously that was not going to work. Mrs. Sisul loves us and thinks 5th grade is pretty great, but we were sure she wasn’t going to help us create a meal that cost that much–with all of the other things we figured it’d be almost $2000!
Then we had to make some decisions:
Ultimately (while it was a hard decision to make and some actually had their feelings hurt a little), we decided to go with the things that were the most cost-effective: least amount of money for the biggest amount of food. We decided to do sausage snack wraps, which are just little pigs-in-a-blanket, because they made 48 in one batch; party pickles (pickles wrapped in ham with cream cheese inside) also made many servings for not much money; guacamole, although we decided to ditch our original recipe and just use salsa and avocados instead of making it all “from scratch”; and fruit–but we abandoned the dip that was going to go with it and picked things we found in the add that was cheap for a lot (oranges, kiwi and apples).
After we reworked our numbers with our new plan, we were PLEASED to find out that we no longer had a budget proposal of $500, but of only $97.84! And even after whittling it down by 4/5 (fractions, nice right?), we knew we could still get our goodies for less at the store by buying store brands instead of only choosing the major brands that were in the ads.
I can’t wait to tell you about our shopping trip! Yep, you heard me right–we went on a field trip to the grocery store. And we lived to tell about it. 🙂
Ready for Part 5? Check it out here.
Happy New Year! I don’t know about you, but I was able to enjoy 16 days off between 2nd quarter and now and it was FABULOUS! What a great gift to be able to spend two whole weeks with my family! And now I am reenergized and ready to get back into a school groove. 🙂
So you know, if you’ve been here before, that math warm-ups are part of that groove. This week I decided to revisit some older concepts (and by old I just mean beginning of the year–to a 5th grader that’s like an eternity ago!) just to remind them that they still need to know how to do this stuff! Thankfully, most had not forgotten.
Monday
Ok, so I guess I lied about them all being oldies-but-goodies. This one was actually based on a problem from an end-of-unit assessment that pretty much everyone got wrong! I really needed to reiterate the fact that it’s really important to think LOGICALLY when you’re doing math. The answer to that problem that most people said–1/18–doesn’t make ANY sense! How the heck do I make 1/18 of a bow?!
Tuesday
Again, I wanted to make sure they had a solid understanding of the difference and the connection between multiplying and dividing fractions.
Wednesday
Thursday
Friday
This one ended up being a lot easier than I first anticipated. I was really close to making it have the “rules” of being a fraction problem, but decided to give them a try with a less complicated one until they tackled a more difficult one. There were promises for more of these next week where they can stretch their creative math muscles! Can’t wait to see what they do. 🙂
In case you missed Feast Week Part 1, check it out here.
Feast Week was born, and we had decided what (and how) we were going to teach that big, deep list of concepts about fractions. We utilized the UbD template for planning the unit, focusing on what we wanted the outcomes to be and then how we’d get them there.
And then we told our kids about it. And they were BEYOND excited! We were giddy about the plan, and my students were as eager as me to start our fraction work so we could head down the road toward the beginning of the actual Feast Week. And just as we had hoped, this was just the motivation that 81 5th graders needed to get through a really hard unit on fractions.
But first we had to learn about fractions. The unit was broken down into eight big ideas:
1. What are fractions anyway?
2. How are fractions related and equivalent to percents and how can they be used to solve problems?
3. How do you find fractional parts of a group (i.e. what is 2/5 of 30 students)?
4. How do you add and subtract fractions?
5. How can you multiply a whole number by a fraction? What does it mean and why would I need to do it in real life? (As a side note: this one was cool, because it is the same as finding the fractional part of a group–they just didn’t know that back at the beginning of the unit)
6. How can you multiply a fraction by a fraction? What does it mean and why would I need to do it in real life?
7. How can you divide a whole number by a fraction? What does it mean and why would I need to do it in real life?
8. How can you divide a fraction by a whole number? What does it mean and why would I need to do it in real life?
The really fabulous (yes, I know I say that word a lot, and yes, I do it on purpose 🙂 ) thing about this unit was how many times I heard the words “Wow, this is easy!” And how surprised so many kids were that it was easy. For some reason, fractions is a four-letter-word to most people and honestly, I think that’s why so many of us (including me!) had so much trouble figuring them out.
We use Investigations as a math resource in our district, and I have always loved the way it works through math concepts–always starting with the why before showing the how. And it was no different with fractions. We did not start with straight number problems where we colored in pies that were the same amount, or with “this is the algorithm for adding fractions.” We started with the why–or the “what” really. What is a fraction, and how does it relate to percents, which are something that everyone already knows about.
Our fraction unit introduced many graphic organizers for kiddos to use to represent their math thinking, and the first one we used was a 10 by 10 grid. We used it to find fourths (again, going back to something they already know), and figured out what fractions and percents we knew from those: 1/4 is 25%, 2/4 is equivalent to 1/2 and 50%, 3/4 is 75%. Then I blew their minds when I showed them how they could find eighths on the same grid. Yep, even though 8 is not a factor of 100. Again, we had them think about what they knew and how they could use that knowledge to figure out something they didn’t know. (I’ll let you stop right now and see if you can figure out how to do it. Go ahead, I’ll even give you a 10 by 1o grid to use.)
Yeah, so I’m sure you’ve figured it out, but I’ll show you anyhow: If you find fourths, then think about what an 1/8 is. It’s half of a 1/4, right? Yep, 1/4=2/8. Since you know that 1/4 is 25%, then you can easily figure out that 1/8 is the same as 12 1/2%. Now you can use that to figure out the percent that is equivalent to any fourth or eighth, just by adding more of them. 3/8 is 37 1/2% because you know 2/8 (1/4) is 25% and then 1/8 is 12 1/2%. Crazy, right? I LOVE THIS PART!! It’s so freeing to kids who have thought all along that fractions are impossible, too hard for them, some secret that they haven’t been told. But now it’s just another puzzle–and they have the pieces to help them solve it! This fraction/percent equivalence plays a HUGE part in the whole rest of the unit, so we spend lots of time at the beginning working with those numbers in different ways to help get it sold in their minds. They had a chart they used as a resource, as well, throughout the unit. Math doesn’t have to be a mystery. It isn’t something you have to memorize. You have tools and you just have to know when and how to use them!
Another organizer we used were 4 x 6 and 5 x 12 rectangles. They’re arrays, just like the 10 x 10 grids, but work better for other numbers that have factors like 3, 4, 5 and 6 (thirds, fourths, fifths, sixths, etc.). We could use them to find the fractional parts of almost any number that way.
These were used when we moved on to finding thirds and sixths (which you can do with percents, as well, too). These were cool, too, when they figured out that 1/3 was 33 1/3% and that 1/6 is half of that. That’s a crazy question: what is 1/2 of 33 1/3? Wish I would have recorded them figuring out that it’s 16 2/3%. Really. It is. Try it. Here, let me show you:
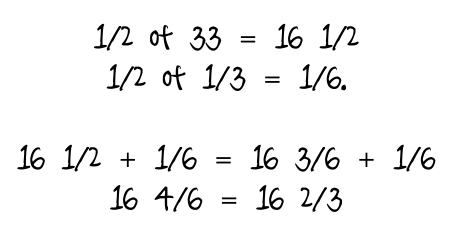
The first time I did that it heard my head. The second and third times it did, too. Yeah, I’ll admit it. Some of the things I ask my kids to do seemed crazy in the beginning. Mainly because it’s not how I learned it, but this time around it totally makes sense. I wonder what it would have been like to do math like this when I was a kid…
(Ready for Part 3? Find it here.)
First of all, Happy New Year! I don’t know when you’re reading this, but I’m writing it during Winter Break, on New Year’s Eve Eve. This is a time of year I both love and hate: the fresh start that comes both personally and professionally in January is one of my favorite things–there is an air of anticipation of new and wonderful things to come; the fact that Spring Break isn’t for another two months is a little disheartening. Winter can be long in Missouri.
That being said, I am excited to tell you a story about what was happening in my classroom–well all the 5th grade classrooms at my school really–during the months of November and December. It was a fun and exciting time in our school, full of learning and anticipation; an eagerness that had nothing to do with holidays or vacations. We were doing hard work, focused on something that at that time seemed like it was forever in the future: Feast Week 2012.
This year I have a whole team full of new friends, and with that comes new ways of doing things–mainly just because we have all done it differently in our previous teaching “lives,” and because we want to plan new things together. So…when it came time to talk about fractions and how we were going to teach that dreaded fabulous unit, we knew it was something we wanted to do together.
First we looked at what we had. I have taught a fraction unit of some sort for the last 7 or 8 years, in 4th and 5th grade. Previously, we really just had to get our friends to a solid understanding of what “fraction” means (part of a whole), and be able to use fraction/percent equivalents to solve problems related to parts of a group. There was also a small part that included adding and subtracting fractions, using the equivalents as the basis (rather than finding common denominators, which is a common practice).
This year, however, our school district is really trying to dig into the new Common Core Standards–hoping to get a feel for what they ask of our kids and how they’ll change things for us as teachers. This is happening most deeply in math; all of our curriculum and rubrics were rewoven to match the CCSS this past summer.
Now, instead of just the basic foundation like I mentioned previously, our kids have to be able to do this:
Can I be honest here for a minute and tell you that we were a little FREAKED OUT by all of that! Unfortunately, until you get to know the CCSS really well, and dig into what they mean and are actually asking your kids to do, I find that they are written in a really complicated way. Needless to say, the first time we even read those expectations we were scared: how were we supposed to get 10- and 11-year-olds to be able to do those things (and do them well, with a deep understanding) if we couldn’t even understand what the standards said?
So after we picked our jaws up off the floor, dried our tears, and got our heart rates back to a somewhat normal rate, we sat down to figure out just how we were going to tackle these things with our students. We began with the belief that they could do it, we could do it and we were going to do it well. We wanted to do it in a meaningful, authentic and real-life way that would help build a “forever and always” understanding, rather than just an “I-get-this-now-but-will-forget-it-after-I-take-the-test-next-week” understanding. That meant rewriting assessments, possibly reworking assignment and activities and rethinking our own working knowledge of fractions.
And so Feast Week was born. It began as an assessment idea, really, but quickly melded into more of a celebration–a culminating activity that would incorporate all that we expected our kids to know and be able to do. It was to take place the last full week before Winter Break, and would include all that goes into creating a Winter Feast–planning, shopping, cooking, and then of course, eating! We based it on an activity I had done in previous years around Thanksgiving where I had students use the circulars from the grocery stores to plan dinner for their family. In that scenario, however, the whole situation was hypothetical. In this reincarnation, it was for real. We set the 5th Grade Fraction Feast to take place as our Winter Party, and the kiddos were entirely responsible for making it happen. Talk about real-life. Authentic. Engaging. Motivating.
And yes, it was. None of it was easy. And yes, I can admit there may have been some tears shed along the way. But we made it, and yes, it was FABULOUS!
Hopefully you’ll hang on for the rest of the story of Feast Week! I promise it’ll be worth your time. 🙂
(**Be sure to read Part 2 here!**)
This week we had five whole days of school! And even better, we had five math warm-ups! Check ’em out!
Monday
Tuesday
This warm-up question illustrates just how authentic and real-life I try to make these. This one really came from a conversation I had with a group as they were working on the problem I gave during work time on Monday. It was just where I wanted us to go, and so presenting it as a warm-up made sense. And when it can be suggested as a kid’s idea instead of mine–which it really was, anyway–that’s even better.
Wednesday
As they did these warm-ups, the focus was on finding common denominators to help them add. Rather than finding the LCM, however, I want them to connect these to work we’ve already done with fraction-percent equivalents; they know they can double or halve certain fractions to make other ones. Mostly we’ve worked with thirds, fourths, fifths, sixths, eighths, and tenths, but I threw that 25 and 50 one in there to see if they could transfer the thinking to a similar problem. They could. 🙂
Thursday
This one reminded (or introduced to some) us of important vocabulary of improper fractions and mixed numbers. As we added these, they focused on changing the mixed number to an improper fraction, adding them, and then reducing it to simplest terms. Notice how the last one has the fraction circled? It was on this problem that someone figured out that we could add the whole numbers and then just add the fractions and put them back together. Smart, huh? Again–this was so much more meaningful that they discovered it on their own, than if I just told them that they could do that as a shortcut.
Friday
These problems encouraged my friends to focus on the strategy we had discovered at the end of the warm-up the day before, and also threw in some vocab we already knew (sums). By the end of this conversation, there some kids who were smiling, which was nice considering all the frowns I’d seen early on in the week. 🙂
On a side note…sorry for the mess of the charts this week. I ran out of chart paper and had to use the backs, too! It’s resourceful, right? Or just messy…not sure which. 🙂
If you read the first post I wrote about Box Factory, then you know about the investigation we finished recently related to volume and surface area.
I think that perhaps one of the most powerful parts of the unit came on the last when each group did a reflection of all that they had accomplished during the unit. I gave them all the posters they had created during our study and asked them to consider these things with their group mates:
They analyzed and discussed, and then went to write their reflections to turn in to me.
It was really great to read about all they’d accomplished during this unit–in their own words. Time after time they mentioned how it was hard at first, but then as they kept trying or as their group mates helped them, they figured it out. They noted how helpful the Math Congress comments were to them, and how these thoughts helped them revise their representations for the next time. They all agreed that this had been a positive experience, and when asked what questions they still had, many said, “When can we do Box Factory again?” 🙂
This week we were working with volume and surface area, so our warm-ups had to do with those topics.
Monday
Tuesday
This one was interesting. I asked it purposely because of the work we had been doing with The Box Factory investigation for the last week–which is all about how to build boxes that hold 24 objects–and was about volume. We hadn’t named it as volume yet, though, and I wanted to see how many people would make that connection. Many of them did not. I saw many “thinking faces” as they struggled with how to answer this one. I heard someone say, “I don’t remember what volume is…” and then several people answered with what it was, but didn’t tell how you’d find it. We had a great conversation about this one, and I heard lots of “oh!” when I told them that they’d been working with volume for a whole week.
Wednesday
This one was again related to the work we’d been doing during Math Workshop. They are used to seeing this kind of equation, since we’d spent a couple of weeks on order of operations recently, and we had been using this kind of equation in our volume work–the parentheses told the equation for the bottom of the box, and the last number told how many layers there were. But I wanted to see if they could explain the formula for finding volume, and tell how they multiplied length x width x height. They don’t need to know this yet, but I thought they were ready for it, so I threw it at them. And many–probably most really–figured it out. We brought the rest of them along through the conversation we had around it.
Thursday
There was not a math warm-up on Thursday because we needed those ten minutes to work on our volume projects.
Friday
The dimensions on this warm-up were from three boxes we’d been working with this week. We’d talked several times about how this was really the same box, turned two different ways to make a new base, so with different dimensions. We’d already talked about the Commutative Property in warm-ups, and so I wanted to see if anyone knew about how this illustrated the Associative Property. Again, a great conversation and many connections were made as we talked. Have I said before how much I LOVE these warm-ups? So many great things happen in just a quick discussion. Love it!
Happy solving! What do you know about volume and surface area? What can you teach us? 🙂
I think I said it in my last post, but golly–being sick is hard! Someone around my house has had a cough for at least a month now, and I’ve had one for at least 2 weeks! Hence my absence from blog-world for that long. All I could stand to do was fall into my bed and sleep when I got home. Luckily, though, I’ve been to the doctor and gotten some medicine and am on the mend. So here I am. 🙂
The horrible thing about not writing for two weeks is that I have a million and one things to post about that have happened, but I’m not really sure how and when I will get them all done–because new things keep getting added everyday! So I guess I’ll start here and see where it takes me.
Last week we were working on division in math, but then added in some practice (an introduction really) with order of operations. Here’s what our warm-ups looked like:
Monday
Tuesday
I was gone and so don’t have a pic of this one, but they solved the problem that they wrote the story for on Monday, using an efficient strategy.
Wednesday
When we started, the red parentheses were not there, and so many were not sure which part to do first. This was the introduction to using order of operations.
Thursday
The original problem is what’s written in pink, and the brown is our work after we talked about how to tackle it.
Friday
I love how complicated this one is! This one tricked many friends, but we’re getting a hang of it now that we’ve done it several days in a row. This was a brand new concept to most mathematicians in my room.
How did you answer our math warm ups? What can you tell us about using Order of Operations to solve problems? Any advice you can give us? Thanks for leaving your comments to help continue our learning. 🙂
We only had two warm-ups this week–more Number Puzzles. This time there were four clues, though, instead of just two. We discussed strategies for where to start and where to go next.
These were great puzzles to help us use our new knowledge of factors and multiples! The kiddos totally rocked. 🙂
20somethingkids and 1kookyteacher 